In this post we’ll learn about binary, hex, and decimal numbering systems. We’ll learn what a ‘base’ is, as well as how to convert these bases to decimal. We’ll also look at why these different number systems are so useful, and some of their most common use cases.
What’s in a base?
In a positional numeral system, the radix or base is the number of unique digits, including the digit zero, used to represent numbers.
Um, thanks Wikipedia. Not the most enlightening is it? Simply put, a “base” is the base set of digits that you can use to represent numbers. So, binary is base 2. The only two digits used to represent numbers in binary are 1 and 0 (there’s two of them). Decimal is base 10 - the digits 0 through 9 make a total of 10 unique digits. Easy right?

The above image shows how we would count from 998 to 1000 in base 10. Once any given column reaches the highest unique value (so in decimal this would be 9), that column becomes zero, and the column to its left is incremented by one (if that column is also the highest digit value, then the next column to the left is incremented). This applies regardless of which base you are using.
Where the “base” part comes in is the little pink squares under each column. The true value of any given column is the column’s value multiplied by the base to the power of the column index (which starts at zero). That sounds complex, but in practice it’s quite simple.
If we assume the number in the above image is decimal, then the x value (in the pink squares) represents the number 10. So reading from left to right, the first column has the value of 1 x (10 ^4), which is equal to 10,000; the next column has the value of 1 x (10 ^ 3), which is 1000. The remaining column values are all zero, so the total value is 11,000. Regardless of what base you are using (decimal, binary, hex etc), the principle remains the same; the only difference is which number you substitute in for the base value.
The number Ten doesn’t exist!
Wait, what? Yeah that’s right. The number “ten” doesn’t actually exist. “Ten” (as well as eleven, twelve etc) is really just a convenient way to describe the number one zero. As soon as you grasp this, understanding how different bases represent numbers becomes much easier.
If you’re still confused, fear not reader! We’ll go over this more in the next few sections.
The different bases
Decimal (base 10)
Decimal, or base 10, is what you’re probably used to dealing with on a daily basis. There are 10 digits used to represent decimal numbers:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binary (base 2)
Binary, or base 2 is the simple yet beautiful numbering system of computers.Everything from numbers, text, and even images can be represented with these two numbers.
Binary has just two unique digits in its number set.
0, 1
As the saying goes - there’s 10 types of people in the world; those who understand binary, and those who don’t.
Hexadecimal (base 16)
Hexadecimal, or base 16, uses sixteen unique digits. You may have already realised “hey wait, we use 16 digits for base 16, but there’s only 10 numeric digits in the Latin alphabet!”. Because we need an additional 6 digits, we use the letters A, B, C, D, E, and F to fill the gap. This is entirely arbitrary however, we could have chosen any 6 letters, or names of fruit, or Simpsons characters, had we chosen to.
1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
While it may sound quite intimidating, hex, is actually more commonplace than you may realise. While often used to condense binary numbers into a more concise representation (among other things), hexadecimal (or hex for short) is also used for color codes in web design - hence hex codes.
For example, #F335B2, which is the hex code for the hot pink color you can see in the diagrams, is actually comprised of 3 groups of hexadecimal numbers: F3, 35, and B2. These 3 groups represent the color values for the red, green, and blue color channels. F3, 35, and B2 equate to 243, 53, and 178 in decimal. We can see then that hex codes can be viewed as a more concise way of representing rgb(243, 53, 178). Isn’t that neat!
Understanding how each base represents numbers
First let’s have a look at some representations of numbers in each base, starting with zero through twenty, and throwing an assortment of larger numbers in for good measure.
Comparison of bases
In the below table, the colored numbers represent the unique set of digits that each base is comprised of.

We can see above that 7 in hex equals 7 in decimal, but 111 in binary. Additionally we can see that D in hex equals 13 in decimal, and 1101 in binary.
You may have noticed binary numbers start getting quite large and unwieldy quite quickly, hence why hex is used commonly as a more concise representation.
What base am I looking at?
You may have noticed that if the number’s base isn’t explicitly stated, it could be easy to interpret a given number using numerous bases.
For example the number 1101 could be one thousand, one hundred and one if the base is decimal, but equally it could be seven if the base is binary.
For this reason, it’s important to denote which base a given number is in. Lucky for you, there is already a standard convention.
- Hexadecimal numbers are represented with a
0xprefix in front of the number. e.g0xAF8 - Binary numbers are represented with a
0bprefix in front of the number. e.g.0b1101 - Decimal numbers are represented without any prefix. So if you can’t see a prefix, you can assume the number is decimal.
Converting to decimal
Regardless of which base you are converting from, the steps are very much the same.
- Annotate each column with the base to the power of the column index (which starts at zero and moves from right to left)
- Convert each single digit to its decimal representation i.e
0xFbecomes15 - Compute the value of each column’s base to the power of its _exponent_s
- Multiply the column value by the result from the previous step
- Add each column value together to get the final result
From Hex
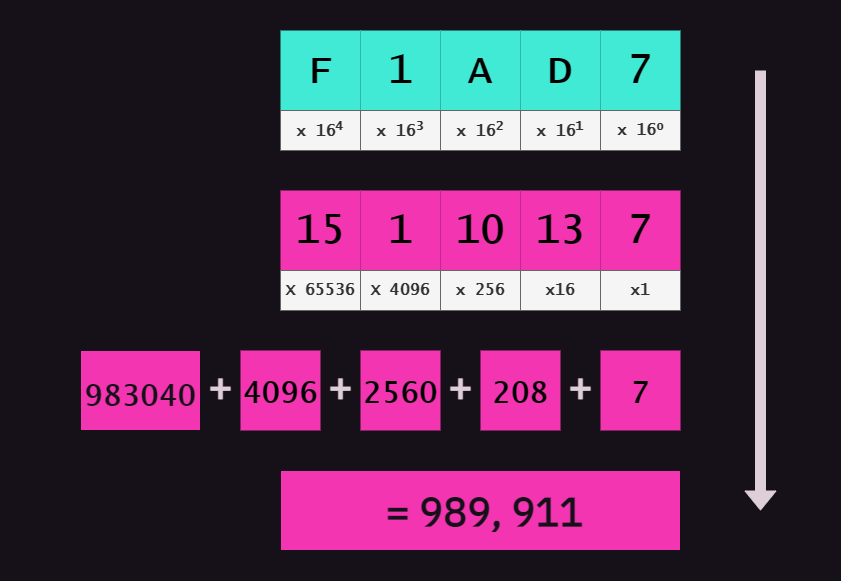
Starting with the hexadecimal number 0xF1AD7:
- Annotate each column with the
baseto the power of the column index (Starting with0at the right hand side). So the column containing theFdigit gets annotated with the value16^4 - Replace each hexadecimal digit with its decimal equivalent. So
Fbecomes15,Dbecomes 13 etc. - For each column, compute the result of the
baseto the power of the column index. - For each column, multiply the above result by the column value
- Sum the totals together
Thus, we can see that 0xF1AD7 in hex is 989,911 in decimal
From Binary
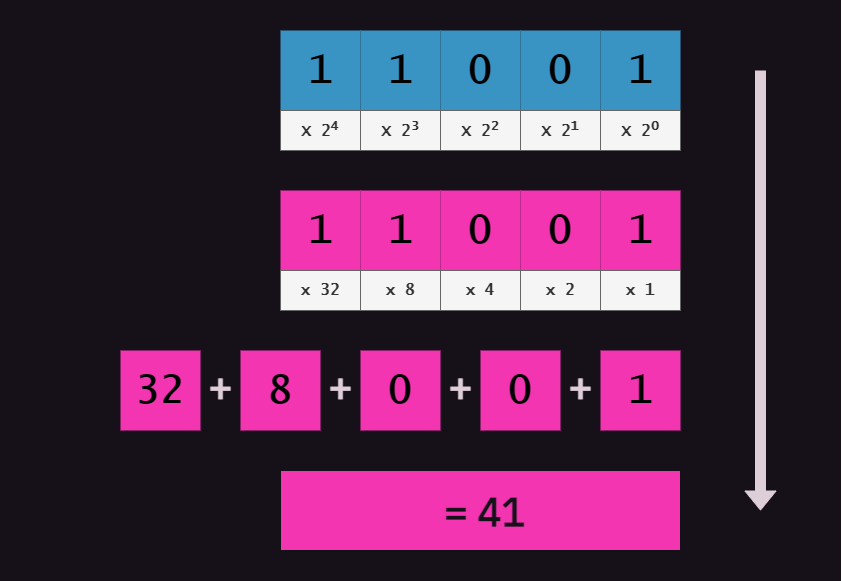
The steps for converting from binary to decimal are no different to the steps described above; in fact, they are even easier. As the value of each column can only ever be a one or a zero, all you need to do is compute the value of the base to the power of the column index for each column, and then sum those results where the column value is not zero.
Converting to other bases
Just using the information described above, you can reverse this process to convert a decimal number to binary or hexadecimal. However, this is somewhat tedious to do manually. I’ll leave it as an exercise to you dear reader, to go forth and discover how to convert decimal numbers to these others using a programmatic formula!
Wrap Up
I sincerely hope you’ve enjoyed this brief foray into the wonderful world of binary and hex, and perhaps now share some of my fascination with the subject. In this blog post., we covered:
- What bases are
- How to interpret different bases
- How binary numbers are represented, and some of their use cases
- How hexadecimal numbers are represented, and some of their use cases
- How to read and convert binary and hex numbers to decimal
Thanks for reading!!
